Ecossistema Python para Computação Numérica
Palestrante: Darlan Cavalcante Moreira
Objetivos
- Aprender como usar a pilha de bibliotecas para computação científica em Python
- Aprender algumas ferramentas eficientes como IPython, Jupyter Notebook, debuggers, etc
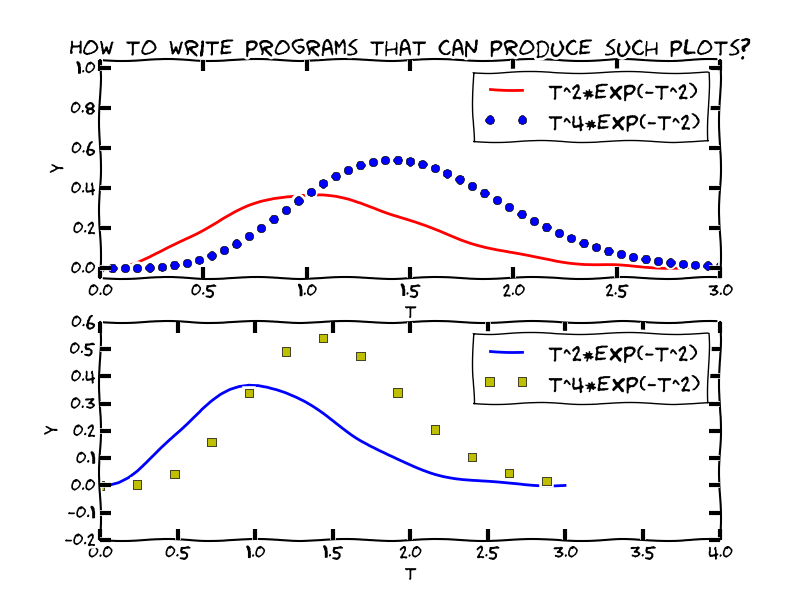
- Aprender a criar plots em Python semelhantes a curva como abaixo
![]()
Qual "bateria" devo usar?
- Python é uma linguagem de programação de uso geral
- O ecossistema para pesquisa científica em Python pode ser visto como diversas camadas que incluem: A linguagem Python, a biblioteca Numpy, bibliotecas baseadas no Numpy, bibliotecas para plot, terminais mais avançados, IDEs e similares
- Nesse curso vamos ver parte dessas ferramentas
Instalando Python
- Python possui duas versões: Python2 e Python3
- Podem baixar a partir do site oficial em https://www.python.org/downloads/
- No windows pode ser complicado instalar bibliotecas e suas dependências
- Um alternativa mais fácil é usar umas das distribuições Python disponíveis:
- Nota: Podem me perguntar sobre o anaconda para mais detalhes depois
IPython
- IPython é poderoso shell interativo para a linguagem Python, muito superior ao shell padrão
- As entradas e saídas são numeradas e você pode recuperar seus valores
- É possível acessar os valores das entradas com variáveis
_i1,_i2, etc - Os valores das saídas podem ser acessadas por
_1,_2, onde_,__e___acessam a última, penúltima e antepenúltima saída
IPython
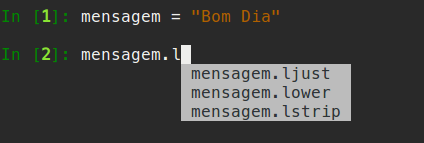
- Um dos recursos mais úteis do IPython é completar um comando
- Após digitar parte do comando aperte TAB para completar
- Caso haja mais de uma opção uma lista de opções será mostrada
- Também acessar o shell do sistema usando
!comando(muito útil para alternar entre pastas, remover arquivos, etc)
IPython
- Obtendo Ajuda com "?"
- Digitar
algum_obj?mostra diversas informações sobre qualquer objeto, incluindo docstring, definições de funções, informações do construtor, etc - Digitar
algum_obj??mostrará o código fonte se possível
abs? Docstring: Return the absolute value of the argument. Type: builtin_function_or_method - Digitar
- Através da introspecção com
?e apertando TAB para completar comandos é possível realmente explorar bem funções, classes, etc.
IPython
- Outro recurso extremamente útil do IPython são os comandos mágicos
- Alguns dos comandos mágicos mais úteis são:
- %whos: Lista variáveis e funções atuais (não mostra variáveis criadas pelo IPython como
_3,_i14, etc) - %edit testando.py: Abre 'testando.py' e executa o código após sair
- %run testando.py: Executa testando.py como um script Também podemos passar opções como "-p" ou "-t"
- %paste: Cola e executa um bloco de código da área de transferência
- %timeit: Executa uma expressão e mostra tempo decorrido
- %autocall: Dispensa os parêntesis em uma chamada de função
- %quickref: Cartão de referência do IPython Veja também
%comando?
a = [1,2,3] b = "Olá Mundo" whos Variable Type Data/Info ---------------------------- a list n=3 b str Hello whos list Variable Type Data/Info ---------------------------- a list n=3 edit testando.py Editing... Waiting for Emacs... cat testando.py # Vamos ver o conteúdo que salvei no arquivo a = 10 b = 20 print(a * b) run testando.py # TAB completa o nome do arquivo 200 whos Variable Type Data/Info ---------------------------- a int 10 b int 20 run -p testando.py Ordered by: internal time ncalls tottime percall cumtime percall filename:lineno(function) 2 0.000 0.000 0.000 0.000 {built-in method io.open} 1 0.000 0.000 0.000 0.000 interactiveshell.py:2431(safe_execfile) 1 0.000 0.000 0.000 0.000 {built-in method builtins.compile} 2/1 0.000 0.000 0.000 0.000 {built-in method builtins.exec} 1 0.000 0.000 0.000 0.000 py3compat.py:182(execfile) 1 0.000 0.000 0.000 0.000 {built-in method builtins.print} 1 0.000 0.000 0.000 0.000 posixpath.py:318(normpath) 1 0.000 0.000 0.000 0.000 posixpath.py:145(dirname) 1 0.000 0.000 0.000 0.000 _bootlocale.py:23(getpreferredenco ... ... ...%timeit 4 * 5 100000000 loops, best of 3: 12.3 ns per loop sum [1,2,3] -------> sum([1,2,3]) - %whos: Lista variáveis e funções atuais (não mostra variáveis criadas pelo IPython como
Jupyter Notebook
- Surgiu inicialmente como IPython Notebook, inspirado pelo Mathematica
- Cada notebook quando aberto está associado a um kernel
- Pode ser usado online em https://try.jupyter.org
- nbviewer: Site com vários notebooks interessantes, como por exemplo esse aqui (versão local)
- Pode ser instalado pelo Anaconda
- Rode o comando
jupyter notebookpara iniciar Tentem agora - Nota: Existem serviços que rodam na nuvem e permitem criar e executar notebooks como SageMathCloud e Wakario
Jupyter Notebook
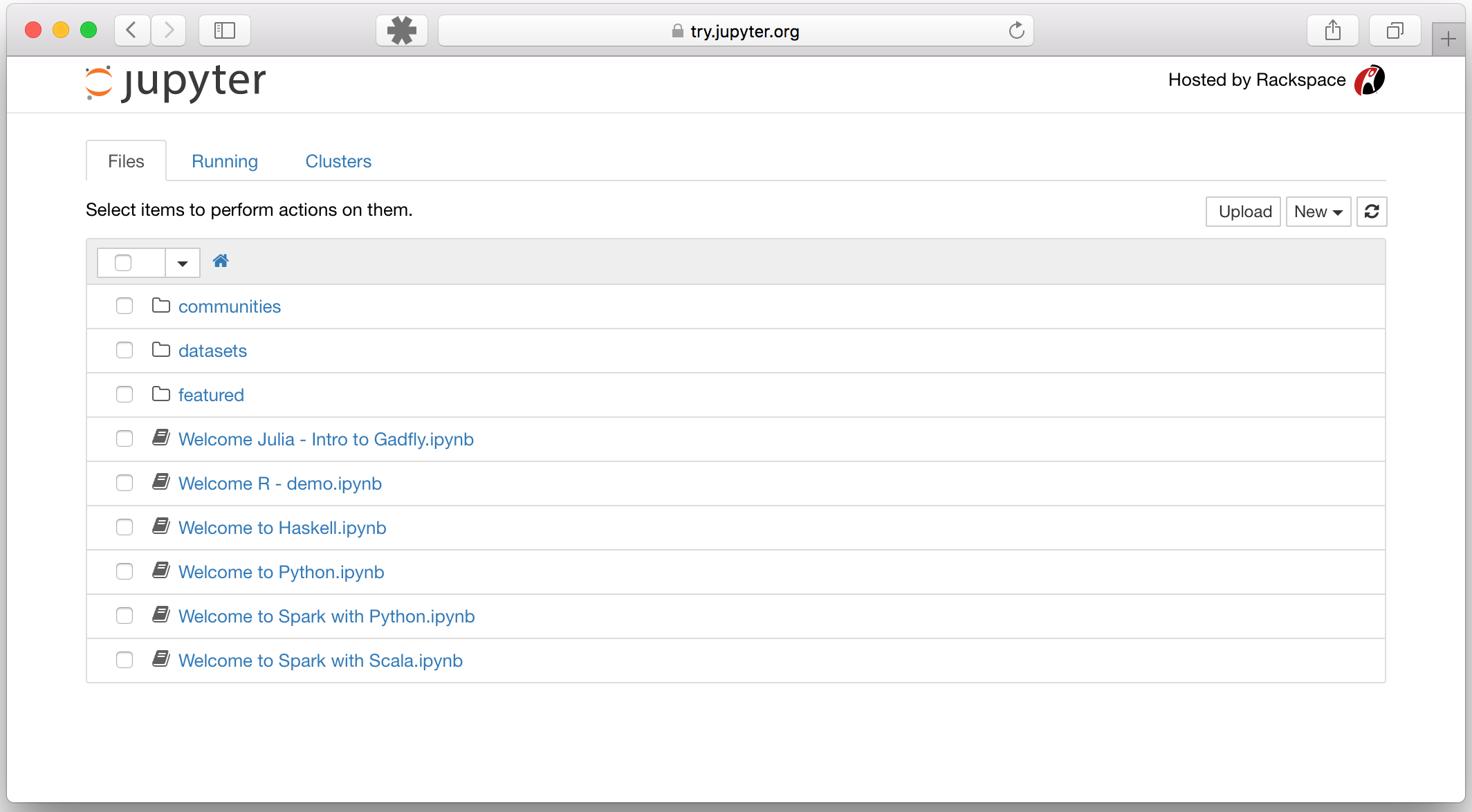
Dashboard
- Ao executar o notebook uma aba do navegador é aberta com o dashboard
- Vemos os arquivos na pasta onde o comando
jupyter notebookfoi executado
Jupyter Notebook
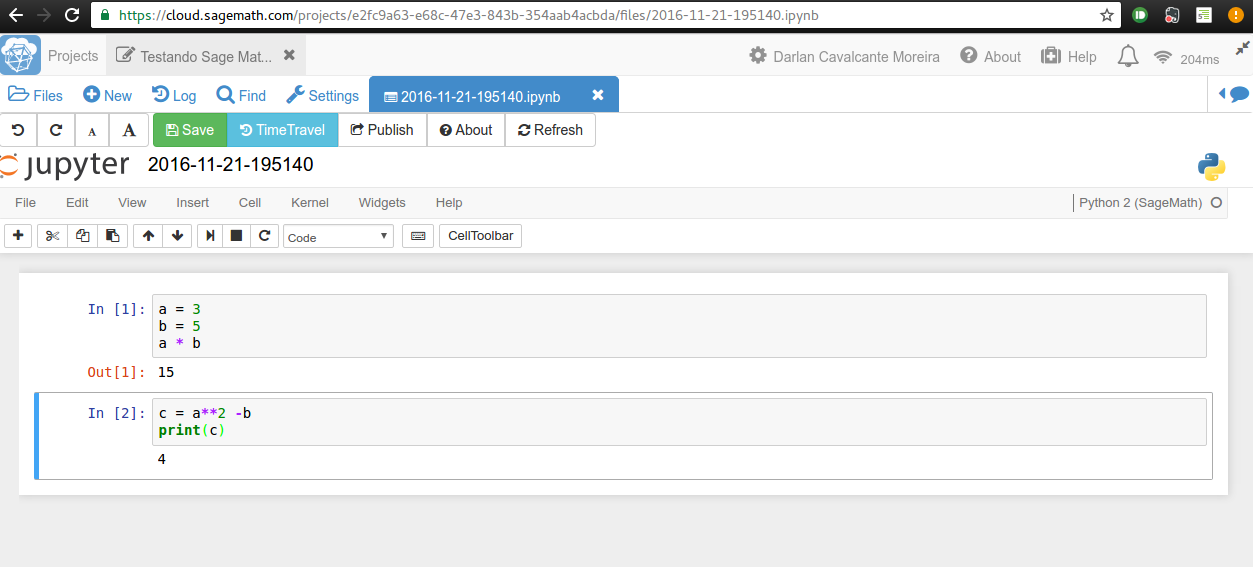
Editor
- No dashboard, cliquem em "New" e escolham o kernel indicado como Python3 para criar um novo notebook
- Executar o tour pela interface em "Help User Interface Tour"
- As células podem ser de dois tipos: markdown e code
- Células do tipo "markdown" contém texto que é renderizado usando a notação markdown
- Células do tipo "code" contém código que será executado, possivelmente resultando em alguma saída mostrada abaixo
- Em alguns caso a saída será mostrada em um formato mais apropriado
Jupyter Notebook
Exercício
- Crie uma célula markdown contendo texto com alguma formatação em markdown
- Uma célula abaixo definindo duas variáveis com números
- Crie uma célula abaixo somando as duas variáveis
- Faça um merge das duas células anteriores
- Crie uma célula vazia
- Delete a célula vazia recém criada
Jupyter Notebook
Mais que um terminal
- O editor do Jupyter possui algumas melhorias que não são possíveis em um terminal
obj?mostra informações do objeto em um pager- Shift+Enter em uma função mostra a docstring da função em um popup
- Rich Display System: Estende o método nativo
__repr__do Python para outras representações e o notebook vai escolher a mais apropriada - Representações possíveis: HTML, JSON, PNG, JPEG, SVG, LaTeX
- Etc.
Numpy Arrays
- Numpy nos fornece um array multidimensional de alto desempenho e ferramentas para trabalhar com esses arrays
- Um array armazena um conjunto de valores, todos do mesmo tipo, e possui um formato (shape)
- O shape de um array é uma tupla de inteiros não negativos e seu número de elementos corresponde ao rank do array
1D numpy array
Shape: (4,)
Tipo: int
2D numpy array
Shape: (2,3)
Tipo: float
3D numpy array
Shape: (4,3,2)
Tipo: int
Criando Arrays
- Existem diversas maneiras de criar um array
- A mais direta é listando seus elementos
Datatype
- Os elementos de um array só podem ser do mesmo tipo
- Um array é muito eficiente em armazenar e
computar se o tipo for
int,float, oucomplex - Podemos verificar o tipo de um array através da propriedade "dtype"
Data Shape
- Podemos verificar o formado de um array através da propriedade shape
- Além da propriedade shape podemos usar size para determinar o número de elementos em um array
- Use o método reshape para mudar o formato do array
Criando Arrays
- Há várias funções que retornam arrays no numpy
- Mais comuns:
zeros,ones,eye,empty
Criando Arrays
- Podemos também criar arrays com valores aleatórios, em um intervalo, etc
Operações Básicas
- Operadores aritméticos em arrays operam elemento-a-elemento
Operações Básicas
- O operador
*não é exceção e efetua uma multiplicação elemento-a-elemento - Para produto matricial use
@ou o métododot
Operações Básicas
- Algumas operações, como
+=e*=, modificam o array atual ao invés de criar um novo array Note que o datatype não pode mudar
with casting rule 'same_kind'
Principais Operações em Arrays
- As diversas funções matemáticas são implementadas como
np.nome_da_funçãoe algumas estão também disponíveis como métodos do array - Experimente digitar "a." no IPython e apertar TAB para ver as sugestões e use "?" para ver o help
Principais Operações em Arrays
- NumPy possui as funções matemáticas usuais: sin, cos, exp, etc.
- Elas são chamadas de "universal functions" (ufuncs)
- Essas funções operam individualmente em cada elemento do array, produzindo um array como saída
Indexando Arrays
- Arrays com uma dimensão podem ser indexados, fatiados, e iterados de forma semelhante a listas
Indexando Arrays
- Arrays multidimensionais podem conter um índice por eixo
- Esses índices são separados por vírgula
- Podemos fornecer menos índices que eixos
- Também podemos usar índices negativos
Indexando Arrays
- Podemos usar também
...para representar tantos ":" quanto necessário para produzir uma indexação completa - Ex: Considere por exemplo um array
xde rank 5 - Temos então que:
x[1,2,...]equivale ax[1,2,:,:,:],x[...,3]equivale ax[:,:,:,:,3]x[4,...,5,:]equivale ax[4,:,:,5,:]- Etc.
Indexando Arrays
- Ao indexar uma dada dimensão o array resultante não possui aquela dimensão, mas para slices a dimensão continua existindo
- Compare os exemplos abaixo (especialmente o shape do resultado)
Indexando Arrays
Vetores Booleanos
- Arrays booleanos podem ser usados para indexar outros arrays
- Isso é especialmente útil para pegar elementos obedecendo certas condições
- Exemplo:
Manipulando o shape
- shape define o número de elementos em cada dimensão
- Há várias maneiras de manipular o shape de um array
- Ao invés de reshape podemos usar resize modifica o array
- Dica: Use "-1" em uma dimensão e o numpy vai detectar o valor correto
Empilhando Arrays
- Vários arrays podem ser empilhados ao longo de um determinado eixo
- Algumas das funções para isso são
hstack,vstack,concatenateestack, np.concatenate
Representação de um Array na Memória
- Um array é armazenado em uma região contínua de memória independentemente de sua dimensão
- Se mudarmos o shape de um array normalmente não é feita uma cópia
- A ordem em que os elementos são armazenados na memória pode tanto ser como "em C" (padrão) ou como "em Fortran"
- Ordem do C: A última dimensão varia mais rapidamente
Representação no NumpyRepresentação na Memória
- Ordem do Fortran: A primeira dimensão varia mais rapidamente
Representação no NumpyRepresentação na Memória
Cópias e Views
- Quando operando e manipulando arrays, as vezes os dados são copiados em um novo array e as vezes não
- Casos sem cópia:
- Assinalamento (Python também funciona assim para tipos mutáveis)
- Mudança de shape
- Argumentos de funções
Cópias e Views
- Diferentes arrays podem compartilhar os mesmos dados na memória
- O método
viewde um array cria um novo objeto array que utiliza os mesmos dados - Mudanças feitas nos dados de um são refletidas no outro array, mas os dois não são o mesmo objeto como ocorre em Python com um assinalamento
- Os dois objetos podem ter formas diferentes
Cópias e Views
- Fatiar um array retorna um view do array
- Para criar um cópia independente de um array use o método
copy
Operações matemáticas
- Já vimos alguns métodos que operam elemento-a-elemento, onde o resultado possui o mesmo rank que a entrada
- Alguns métodos reduzem a dimensão obtendo um resultado de rank menor
- Exemplo:
mean,var,sum, etc. - É possível indicar sobre qual dimensão efetuar a operação
Broadcast
- Operações no NumPy geralmente são feitas em pares de arrays elemento-a-elemento
- Broadcast corresponde a maneira como o numpy trata arrays com formas diferentes durante operações aritméticas
- O exemplo mais simples de broadcast ocorre quando um array e um escalar são combinados
- o escalar é esticado durante a operação aritmética para ter a mesma forma que o array
Broadcast
- Além da praticidade o broadcast fornece outras vantagens:
- É um meio de vetorizar operações com arrays tal que os loops ocorram em C, ao invés de Python
- Sem cópias desnecessárias dos dados implementações eficientes de algoritmos
- Exemplo: somar uma matriz (3,3) com um vetor (3,)?
- Adicionamos uma dimensão extra no vetor novo shape de (1, 3)
- Replicamos o "vetor" para ter o mesmo shape que a matriz (3,3)
Broadcast
- Para o broadcast ser possível duas regras precisam ser atendidas:
- Regra 1: Se os arrays de entrada possuem ranks diferentes adicione uma dimensão no início do array menor repetidamente até que os dois tenham o mesmo rank
- Regra 2: Arrays de tamanho 1 em um dada dimensão atuam como se eles tivessem o mesmo tamanho que o array de maior tamanho nessa dimensão
- Após a aplicação das duas regras anteriores as dimensões dos dois arrays devem bater
Broadcast
Exemplos
- Muito mais que operações entre um array e um simples escalar
- Nem sempre as dimensões coincidem após aplicar as duas regras
- Se for o caso você pode manualmente adicionar um eixo novo para não depender da regra 1
Broadcast
Exercício
- Dado o vetor de números complexos abaixo representando posições de pontos em um grid 2D, calcule as distâncias de cada ponto para cada outro ponto no grid.
pontos = np.array([-2+1j, 3+2.5j, 2-2j, 0, 1.5+2.7j])Álgebra Linear
- Numpy fornece diversos métodos para manipulação de matrizes de maneira eficiente
- Por baixo dos panos bibliotecas eficientes como BLAS e LAPACK são utilizadas, tornando operações de álgebra linear eficiente
- Algumas das operações mais comuns são:
Plotando com Matplotlib
- A biblioteca mais conhecida para plot no Python é a Matplotlib
- A função mais importante é a função
plt.plot, que recebe arrays com os valores para plotar - Chame a função
plt.showno final para mostrar o plot - Com um pouco esforço a mais podemos facilmente plotar múltiplas linhas de uma só vez, adicionar um título, legenda e labels para os eixos
- Dica: coloque
%matplotlib inlineou%matplotlib notebookna primeira célula do Jupyter notebook
import numpy as np
import matplotlib.pyplot as plt
# Computa as coordenadas 'x' e 'y' para ambas as curvas
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
# Plota os pontos usando matplotlib
plt.plot(x, y_sin)
plt.plot(x, y_cos)
plt.xlabel('x axis label')
plt.ylabel('y axis label')
plt.title('Sine and Cosine')
plt.legend(['Sine', 'Cosine'])
plt.show() # Necessário para mostrar o gráfico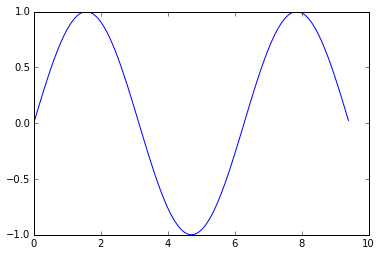
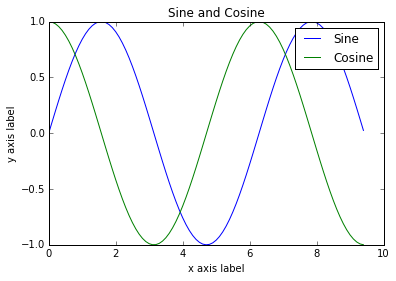
Plotando com Matplotlib
Exercício
- Repita o plot anterior no notebook, mas agora incluindo círculos nos pontos
- Dica: rode o comando plt.plot? para ver a ajuda do comando
Plotando com Matplotlib
- Podemos plotar curvas diferentes na mesma figura usando a função
subplot - Na documentação há muito mais que se pode fazer com subplots
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
# Prepara um grid 2x1 para subplots e ativa o primeiro subplot
plt.subplot(2, 1, 1)
# Cria o primeiro plot
plt.plot(x, y_sin)
plt.title('Sine')
# Ativa o segundo plot do grid e cria o segundo plot
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title('Cosine')
plt.show()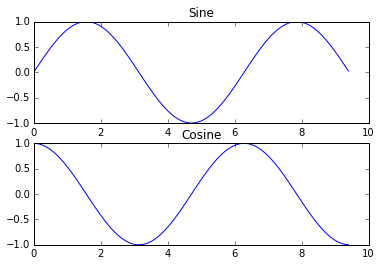
Mostrando imagens com Matplotlib
- Matplotlib também possui a função
imshowque pode ser usada para mostrar uma imagem - Aqui usamos a função
imreaddo scipy para ler a imagem
import numpy as np
from scipy.misc import imread, imresize
import matplotlib.pyplot as plt
img = imread('assets/cat.jpg')
img_tinted = img * [1, 0.95, 0.9]
# Mostra a imagem original
plt.subplot(1, 2, 1)
plt.imshow(img)
# Mostra a imagem modificada
plt.subplot(1, 2, 2)
# Nota: imshow resulta em resultados estranhos se os dados
# não são uint8. Para contornar esse problemas fazemos um
# cast da imagem para uint8 antes de mostrá-la
plt.imshow(np.uint8(img_tinted))
plt.show()

Exercícios de Fixação
- Crie uma matriz A com dimensão 3 × 4 de números inteiros menores que 10
- Calcule a matriz transposta de A
- Calcule a soma de cada linha da matriz A usando a função sum
- Calcule a soma de cada coluna da matriz A usando a função sum
- Calcule a pseudo-inversa \(A^\dagger = A^T(AA^T)^{-1}\)
- Defina B = AA T e calcule os autovalores e os autovetores de B usando a função eig
- Calcule a inversa de B usando a função inv